Beyond ResNet: How DeepSeek's mHC Solves the 'Exploding Highway' Problem

For over a decade, the architecture of deep neural networks has been built on a foundational principle: the Residual Connection, introduced by ResNet. This simple addition of a signal “highway” from one layer to the next preserved the Identity Mapping Property, ensuring that signals could flow unimpeded through hundreds or thousands of layers. This stability was the key to training increasingly deep and powerful models.

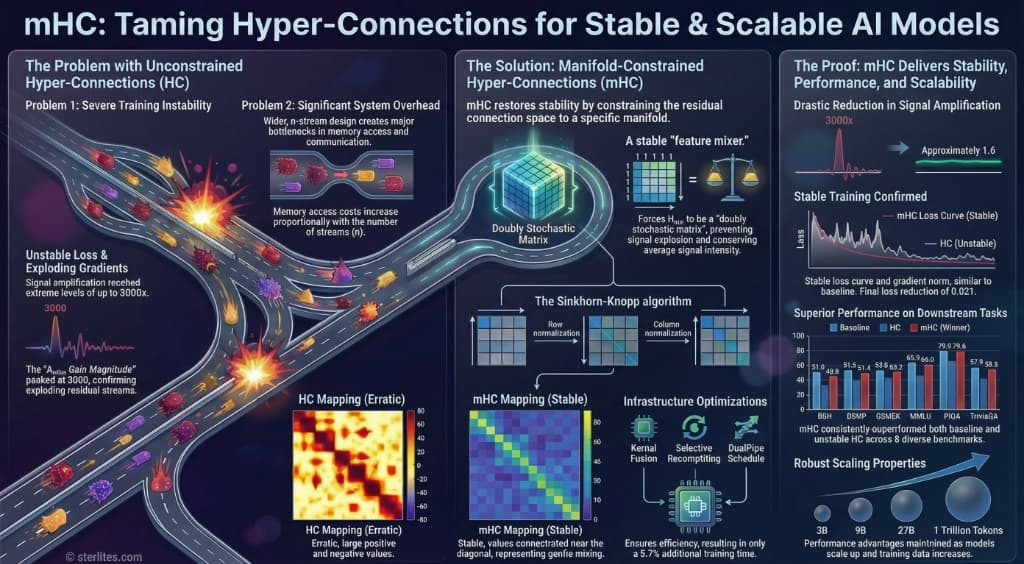
An ambitious successor, Hyper-Connections (HC), attempted to supercharge this design by widening the residual highway from a single lane into a multi-lane superhighway. The goal was to increase the network’s topological complexity and information capacity without a proportional increase in computational cost. However, this promising approach introduced a critical flaw: it broke the identity mapping property. The learnable matrices used to mix signals between the new lanes were unconstrained, leading to a phenomenon that can be termed the “exploding highway”—unbounded signal amplification that severely destabilized large-scale models.

The elegant solution comes from DeepSeek AI in the form of Manifold-Constrained Hyper-Connections (mHC). This method restores the crucial training stability lost by HC. Its core function is to project the residual connection matrices onto a specific mathematical manifold called the Birkhoff Polytope. This geometric constraint recovers the identity mapping property, taming the exploding signals while retaining the high-capacity benefits of a widened residual stream.

To understand why Hyper-Connections became unstable at scale, it is essential to first grasp the principle they broke.

What is the Identity Mapping Property? This property is the cornerstone of ResNet’s success in training very deep networks. The source paper defines it as “the property that the signal from the shallower layer maps directly to the deeper layer without any modification.” This ensures a baseline identity path exists, guaranteeing that the network can, at a minimum, learn to pass the input through without degradation, which is critical for gradient flow in deep models. This direct, unimpeded signal flow is what prevents signals from vanishing or exploding, a common failure mode in extremely deep architectures.

Hyper-Connections (HC) attempted to improve on ResNet by expanding the single residual stream into multiple parallel streams (e.g., n streams). It introduced learnable matrices (H_res) to mix signals between these streams at each layer, aiming to create a richer flow of information. The critical failure was that these H_res matrices were completely unconstrained. When applied sequentially layer after layer, the composite mapping (∏H_res) destroyed the identity mapping, distorting and amplifying the signal uncontrollably.

This failure is quantified by the “Amax Gain Magnitude” metric, which measures the worst-case signal expansion. Crucially, this metric captures instability in both directions: its forward-pass component (based on maximum absolute row sums) measures signal explosion, while its backward-pass component (based on maximum absolute column sums) corresponds to exploding gradients. As documented in the paper’s analysis, the unconstrained HC architecture caused “exploding residual streams,” with the pile-up on the exploding highway reaching extreme peaks of approximately 3000. This severe deviation confirms the identity mapping was destroyed, leading to numerical instability during training.

The mHC method introduces principled, geometric guardrails to solve the instability of HC while preserving its high-capacity benefits.

The central insight of mHC is to constrain the learnable residual mapping matrix (H_res) so that it facilitates robust information exchange between streams without amplifying or diminishing the overall signal energy. It enforces a strict “conservation of signal” property.

To achieve this, mHC relies on key technical components:

• Birkhoff Polytope (Doubly Stochastic Matrices): The mHC framework projects the H_res matrix onto this specific mathematical manifold. A matrix on the Birkhoff Polytope is “doubly stochastic,” meaning it contains only non-negative entries and all of its rows and columns sum to 1. This provides a powerful geometric interpretation: the mapping acts as a “convex combination of permutations.” This not only robustly mixes features across streams without changing the overall signal norm, but as the source paper notes, “the repeated application of such matrices tends to increase the mixing of information across streams monotonically, effectively functioning as a robust feature fusion mechanism.”
• Sinkhorn-Knopp Algorithm: This is the specific iterative algorithm used to enforce the doubly stochastic constraint. The algorithm alternately rescales the rows and columns of the H_res matrix until they all sum to 1, effectively projecting the unconstrained matrix onto the stable Birkhoff Polytope. The experiments detailed in the paper use 20 iterations (t_max = 20) to achieve this.

The impact of installing these geometric guardrails is dramatic. As detailed in the Stability Analysis section of the paper, mHC drastically reduces the “Amax Gain Magnitude” from HC’s chaotic peak of ~3000 to a tightly controlled maximum value of approximately 1.6. This demonstrates that the identity mapping property has been effectively recovered, ensuring stable signal propagation through the entire network.

The theoretical stability of mHC translates directly into practical gains in large-scale model training. Experiments on a 27B Mixture-of-Experts (MoE) model demonstrate its effectiveness.

mHC successfully mitigates the training instability seen in the HC architecture, achieving a stable gradient norm comparable to the baseline ResNet model. Simultaneously, it achieves a final training loss that was 0.021 points lower than the baseline ResNet, a significant improvement in convergence for a model of this scale.

This improved training stability leads to superior performance on downstream tasks. According to the benchmark results, the mHC-trained model demonstrates enhanced reasoning capabilities, with notable gains of 2.1% on BBH and 2.3% on DROP compared to the unstable HC model, which itself showed gains over the baseline but was hampered by training volatility.

For years, scaling AI models has been a story of “Brute Force Scaling”: achieving better performance by simply adding more parameters and throwing more FLOPs at the problem. While effective, this approach is hitting fundamental economic and thermodynamic limits.

Geometric scaling offers a path to greater capability with more sustainable resource growth, making it a critical research direction for the next decade of AI. It allows architects to increase the model’s ability to carry and mix rich information through its layers without being forced to pay the full price in FLOPs that would come from simply making the core attention and FFN blocks wider.

A key aspect of mHC is its practicality. It restores stability and improves performance with only ~6.7% additional training time overhead. This remarkable efficiency underscores a critical insight: the frontier of AI architecture is now inseparable from the frontier of systems engineering.

Architectural innovations like mHC are only viable because of co-designed, low-level optimizations. To make advanced architectures computationally feasible, DeepSeek developed custom compute kernels using TileLang, a specialized programming model for AI systems. This tool fused multiple operations into unified kernels, minimizing memory bandwidth bottlenecks—a critical factor for runtime efficiency. Without this deep co-design, mHC would be a theoretical curiosity, not a production-ready advantage.

DeepSeek’s mHC solves the critical instability problem of Hyper-Connections by applying a principled geometric constraint. By projecting connection matrices onto the Birkhoff Polytope, it transforms the residual update into a stable convex combination of feature streams, preserving signal energy while promoting robust information mixing. It effectively restores the identity mapping property that has been essential to deep learning for a decade.

As a flexible and practical extension of the residual connection paradigm, mHC opens promising avenues for future research into macro-architecture design. The exploration of other geometric constraints could lead to novel methods that further optimize the trade-off between a model’s stability and its capacity, potentially illuminating new pathways for the evolution of next-generation foundation models.